Posterior Inference in Sequential Models with Soft Value Guidance

Fine-tuning, controlled generation, and sampling in sequential models has attracted a flurry of recent attention in a variety of settings, particularly with the growing availability of powerful open-source pretrained models. For language modeling in discrete spaces, we would often like to align responses with human preferences or generate correct responses to complex reasoning questions. For diffusion models, we may be interested in steering generation to produce samples belonging a certain class, images which score highly on metrics such as realism, preference alignment, or text-to-image consistency, and proteins or molecules with desired properties such as synthesizability. In all cases, we can imagine the task as sampling from a target probability distribution only known up to its unnormalized density or energy function. Sampling from arbitrary target probability densities such as Boltzmann distribution of physical systems is itself a famous and difficult problem, for which diffusion-based samplers have recently been an active area of interest.

In this blog post, we draw on a rich history of work viewing stochastic control or reinforcement learning as probabilistic inference , in order to provide a conceptual framework for recent developments in fine-tuning, guidance, alignment, and sampling using language and diffusion models with sequential structure. A key role is played by the soft value function, which summarizes future information relevant to sampling from a target posterior at intermediate steps. Further, we highlight that the optimal soft value function provides potentials for Sequential Monte Carlo resampling and the desired gradient guidance for diffusion processes. This perspective allows drawing connections between methodologies used in various problem settings across both discrete and continuous spaces.

Setting & Notation

Assume we are given a pretrained model \(p^{\text{ref}}\), which we will eventually seek to condition or modulate to achieve some target properties or distribution at the endpoint. The reader should feel free to skip ahead to concrete examples in Target Distributions and parse the notation within this context.

We first cast autoregressive language models within a Markovian structure, which will be used to provide shared notation for diffusion and language models in later exposition. We consider the state \(\mathbf{x}_{t} = \mathrm{concat}({\mathbf{x}_{0}}, x_{1}, x_{2}, \ldots x_{t}) \in \mathcal{V}^{T_{0}+t}\) in an expanding state-space of tokens \(x_{\tau} \in \mathcal{V}\) from a discrete vocabulary, which are generated in response to a prompt or initial state \(\mathbf{x}_{0} \in \mathcal{V}^{T_{0}}\) of maximum length \(T_{0}\). We view a reference policy \(p^{\text{ref}}_{\text{LM}}(a_t = x_{t+1} \vert {\mathbf{x}_t})\) as selecting a next token \(x_{t+1}\) as the action \(a_t\) with the context \(\mathbf{x}_t\) as the state , with deterministic environment transitions \(p^{\text{env}}(\mathbf{x}_{t+1} \vert a_t = x_{t+1}, \mathbf{x}_t) = \mathbb{I}[\mathbf{x}_{t+1} = \text{concat}(\mathbf{x}_t, x_{t+1})]\) that concatenate the generated token \(x_{t+1}\) with the context \(\mathbf{x}_t\). The policy is usually given by an autoregressive model \(\mathbf{x}_t \sim \prod_{\tau=0}^{t-1} p^{\text{ref}}_{\text{LM}}(x_{\tau+1} \vert \mathbf{x}_{\tau})\) . For convenience, we will write the full state transition as \(p^{\text{ref}}_{t+1}(\mathbf{x}_{t+1} \vert \mathbf{x}_{t})=p^{\text{ref}}_{\text{LM}}(x_{t+1} \vert \mathbf{x}_t) \mathbb{I}[\mathbf{x}_{t+1} =\text{concat}(\mathbf{x}_t, x_{t+1})]\) . This leads to a slight abuse of notation in which we can write the probability of a (partial) sequence $\mathbf{x}_t$ either using tokens \(p^{\text{ref}}_t(\mathbf{x}_t)=\prod_{\tau=0}^{t-1} p^{\text{ref}}_{\text{LM}}(x_{\tau+1} \vert \mathbf{x}_{\tau})\) or as a joint distribution over its prefixes \(p^{\text{ref}}_{t}(\mathbf{x}_{0:t}) = \prod_{\tau=0}^{t-1} p^{\text{ref}}_{\tau+1}(\mathbf{x}_{\tau+1} \vert \mathbf{x}_{\tau})\) .

For diffusion processes, let \(\mathbf{x}_t \in \mathbb{R}^d\) represent the current (noisy) state, where \(\mathbf{x}_T\) corresponds to clean data. We focus on continuous diffusion models here. While many concepts introduced will be relevant to discrete diffusion guidance, this remains an active area of research. We consider a reference stochastic differential equation with time-dependent drift \(b_t^{\text{ref}}\) , which may correspond to a physical force or pretrained score-based diffusion model

\(\begin{align} P^{\text{ref}}: \qquad d \mathbf{x}_t = b_t^{\text{ref}}({\mathbf{x}_t}) dt + \sigma_t dW_t \qquad {\mathbf{x}_{0}} \sim p_{0}^{\text{ref}} \end{align}\)

We can approximately model this continuous-time stochastic processes using discrete-time Gaussian kernels for small \(dt\) . We consider the reference drift as an action \(a_t = b_t^{\text{ref}}(\mathbf{x}_t, t)\) , with stochastic environment transitions drawn from \(p^{\text{env}}(\mathbf{x}_{t+1} \vert a_t = b_t^{\text{ref}}(\mathbf{x}_t,t), \mathbf{x}_t)= \mathcal{N}(\mathbf{x}_{t+1}; \mathbf{x}_t + b_t^{\text{ref}}(\mathbf{x}_t)dt , \sigma_{t} \mathbb{I}_d)\) via Euler discretization. For convenience, we combine action selection and state transition into the policy \(p^{\text{ref}}_{t+1}(\mathbf{x}_{t+1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t+1}; \mathbf{x}_t + b_t^{\text{ref}}(\mathbf{x}_t)dt, \sigma_{t} \mathbb{I}_d)\) .

Posterior Conditioning in both Language and Diffusion Models. See Soft Value Function and Stochastic Optimal Control sections for the role of the value function.

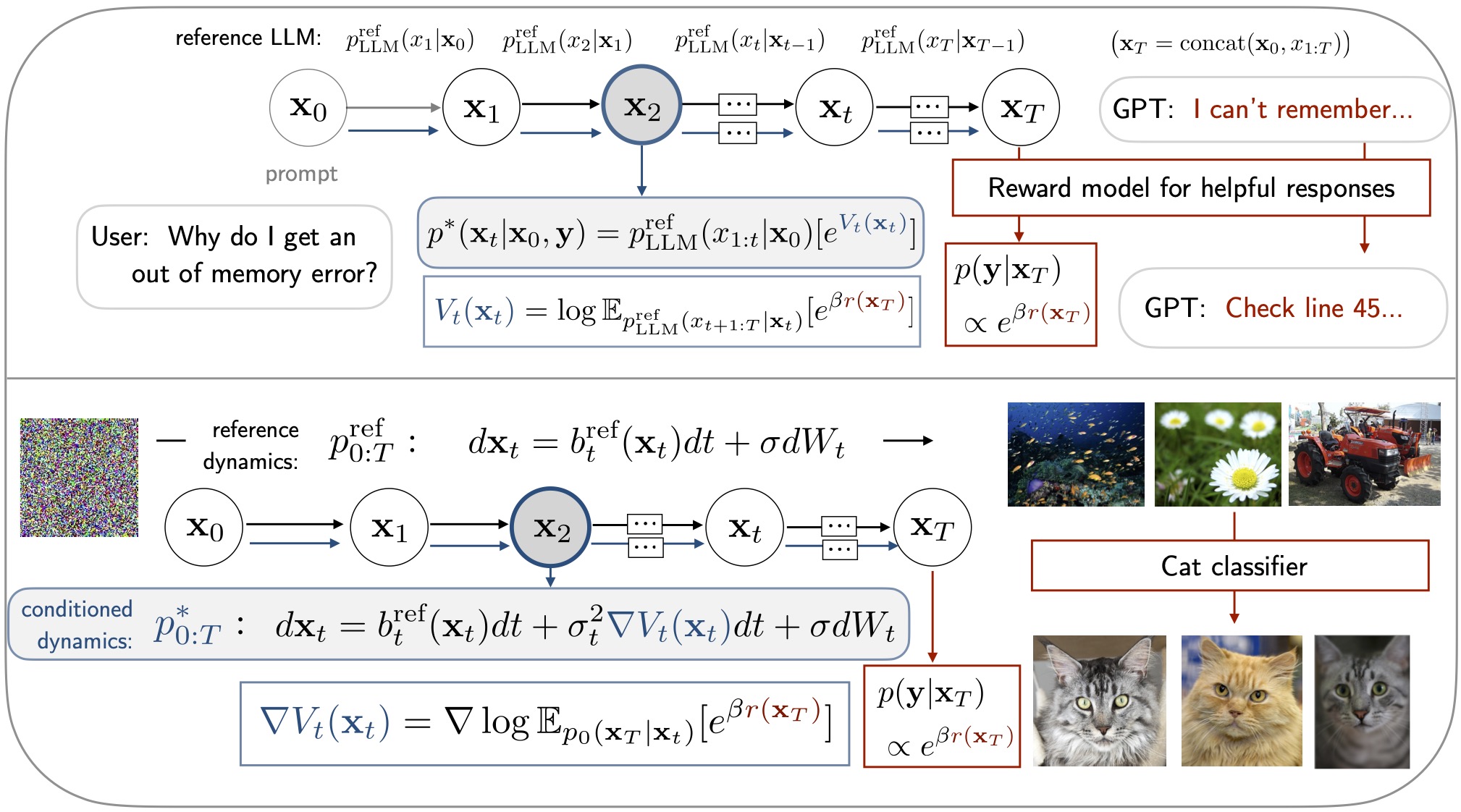
Target Distributions

We will proceed to view many controlled generation or fine-tuning tasks as sampling from a target probability distribution at the final step \(T\) , where the target is only known up to a normalization constant.. Compared to generative modeling, this task can be notably more difficult since we do not have access to samples from the target distribution.

To ease notation and facilitate posterior sampling interpretations, we define an observation random variable \(\mathbf{y}\), which is emitted as a function of the final state according to \(p(\mathbf{y} \vert \mathbf{x}_T)\), and attempt to sample from the posterior distribution over all states,

\[\begin{align} p^*(\mathbf{x}_{0:T} \vert \mathbf{y}) = \frac{1}{\mathcal{Z}^\mathbf{y}} p^{\text{ref}}(\mathbf{x}_{0:T})p(\mathbf{y} \vert \mathbf{x}_T) \quad \qquad \mathcal{Z}^\mathbf{y} =\int p^{\text{ref}}(\mathbf{x}_{0:T})p(\mathbf{y} \vert \mathbf{x}_T) d\mathbf{x}_{0:T} \label{eq:tgt} \end{align}\]

In particular, we would like our full language model responses or final diffusion states to be distributed according to the endpoint posterior marginal \(p^*(\mathbf{x}_{T} \vert \mathbf{y})\). We will consider a flexible class of possible target posteriors defined in the following table.

Setting	\(p(\mathbf{y} \vert \mathbf{x}_T)\)	\(p^*(\mathbf{x}_{T} \vert \mathbf{y})\)
Constraint	\(\mathbb{I}[\mathbf{x}_T \in \mathcal{B}]\)	\(\frac{1}{\mathcal{Z}^{\mathcal{B}}} p^{\text{ref}}(\mathbf{x}_{T})\mathbb{I}[\mathbf{x}_T \in \mathcal{B}]\)
Classifier or Observation	\(p(\mathbf{y} \vert \mathbf{x}_T)\)	\(\frac{1}{\mathcal{Z}^\mathbf{y}} p^{\text{ref}}(\mathbf{x}_{T})p(\mathbf{y} \vert \mathbf{x}_T)\)
Reward or Energy Modulation	\(\frac{1}{M}\exp\{ \beta~ r(\mathbf{x}_T) \}\)	\(\frac{1}{\mathcal{Z}^{\beta r}} p^{\text{ref}}(\mathbf{x}_{T})\exp\{ \beta~ r(\mathbf{x}_T) \}\)
Arbitrary Unnormalized Density	\(\frac{1}{M}\frac{\tilde{\pi}_T(\mathbf{x}_T)}{p^{\text{ref}}(\mathbf{x}_T)}\)	\(\frac{1}{\mathcal{Z}} \tilde{\pi}_T(\mathbf{x}_T)\)

A crucial challenge arises from the fact that conditioning information is only provided at the terminal state \(\mathbf{x}_T\) , whereas generation or sampling needs to be performed sequentially and forward in time according to

\[\begin{align} p^*(\mathbf{x}_{0:T} \vert \mathbf{y})= p^*(\mathbf{x}_{0} \vert \mathbf{y}) \prod_{t=1}^{T} p^*(\mathbf{x}_{t} \vert \mathbf{x}_{t-1}, \mathbf{y}) \label{eq:backward} \end{align}\]

Before describing how soft value functions and stochastic optimal control can be used to address this challenge, we discuss several concrete examples below.

Examples

Constraints

For the language modeling setting, constraints may filter responses which correspond to correct answers to reasoning questions , syntactically-valid outputs, or responses for which a scalar function meets an acceptability or rare-event threshold \(\mathbb{I}[ f(\mathbf{x}_T)\leq c]\).

For diffusion modeling, constraining the endpoint sample to fall within a certain set \(\mathbb{I}[ \mathbf{x}_T \in \mathcal{B}]\) corresponds to the traditional formulation of Doob’s $h$-transform, which has been used for generative modeling on constrained domains or with aligned data arising in biomolecular or chemical problems. In the case where \(p^{\text{ref}}\) is a diffusion with linear drift, the conditioned process ending at a particular point \(\mathbb{I}[ \mathbf{x}_T = \mathbf{x}]\) is available as a closed form linear interpolation. This observation underlies efficient optimization techniques for `bridge matching’ methods which extend rectified flow matching to stochastic processes and Schrödinger Bridge problems for generative modeling or image translation. The solution to the Schrödinger Bridge (SB) problem can be viewed as a controlled diffusion in the form of \eqref{eq:csde} and \eqref{eq:soft_value_drift}, where the control drift $u_t$ becomes a posterior expectation of the reference transition probability $$ \begin{align*} u_t(\mathbf{x}_t)= \sigma_t^2 \nabla_{\mathbf{x}_t} \log p^*(\mathbf{y}|\mathbf{x}_t) &= \sigma_t^2 \int d\mathbf{x}_T \frac{p^{\text{ref}}(\mathbf{x}_T|\mathbf{x}_t) p(\mathbf{y}|\mathbf{x}_T)}{\int p^{\text{ref}}(\mathbf{x}_T|\mathbf{x}_t) p(\mathbf{y}|\mathbf{x}_T) d\mathbf{x}_T} \nabla_{\mathbf{x}_t} \log p^{\text{ref}}(\mathbf{x}_T|\mathbf{x}_t) \\ &= \sigma_t^2 \mathbb{E}_{p^*(\mathbf{x}_T|\mathbf{x}_t,\mathbf{y}=1)}[ \nabla_{\mathbf{x}_t} \log p^{\text{ref}}(\mathbf{x}_T|\mathbf{x}_t)] \end{align*}$$ While this fits into the General Unnormalized Target Density setting above, we do not emphasize this example since the SB problem usually assumes access to samples only. See for discussion, where the Sinkhorn algorithm is used to obtain a likelihood ratio ($\propto p(\mathbf{y}|\mathbf{x}_T)$) from samples and construct the control drift $ u_t $.

Classification or Observation Random Variables

Given a classifier \(p(\mathbf{y}=c | \mathbf{x}_T)\), we can hope to condition our language or diffusion model to generate samples likely to be of a certain class, such as uncovering language model responses which are flagged by content moderation classifiers. In the Stochastic Optimal Control section below, we will see that class-conditioned diffusion processes characterize the optimal form of well-known guidance techniques . Finally, conditioning on a noisy observation \(\mathbf{y}= \mathcal{A}(\mathbf{x}_T) + \epsilon\) is natural for solving inverse problems in imaging .

Reward or Energy Modulation

Reinforcement learning from human feedback has become a dominant paradigm for aligning pretrained language models with human preferences or task-specific applications , finetuning diffusion models to align with text prompts or user feedback , or generating proteins, molecules, or genetic sequences with particular properties such as stability, synthesizability, or downstream effectiveness . For our purposes, we will assume a reward model is given.

General Unnormalized Target Densities

Most generally, we can seek to sample from a given target distribution over the final state \(\pi_T(\mathbf{x}_T) \propto \tilde{\pi}_T(\mathbf{x}_T)\), which is given only via its unnormalized density \(\tilde{\pi}_T(\mathbf{x}_T)\). This includes reward modulation \(\tilde{\pi}_T(\mathbf{x}_T) = p^{\text{ref}}(\mathbf{x}_{T})\exp\{ \beta~ r(\mathbf{x}_T) \}\) or Boltzmann distributions as special cases.

To facilitate a posterior interpretation in these cases, we would like to introduce a random variable \(\mathbf{y}\) which reflects `optimality’, or the fact that endpoint samples are distributed according to the endpoint target. We thus construct a hypothetical rejection sampling of the endpoint samples, where we accept samples with probability \(p(\mathbf{y}=1 \vert \mathbf{x}_T) = \frac{1}{M}\frac{\tilde{\pi}_T(\mathbf{x}_T)}{p^{\text{ref}}(\mathbf{x}_T)}\), for \(M = \max \limits_{\mathbf{x}_T}\frac{\tilde{\pi}_T(\mathbf{x}_T)}{p^{\text{ref}}(\mathbf{x}_T)}\). The constant \(M\), which ensures \(p(\mathbf{y}=1 \vert \mathbf{x}_T) \leq 1\) and that accepted samples have the desired distribution, need not be estimated in practice, since it can be shown to vanish in the eventual posterior \(p^*(\mathbf{x}_T \vert \mathbf{y}=1)\). (see derivations here In detail, consider only the final step posterior for simplicity $$ \begin{align*} p^*(\mathbf{x}_T|\mathbf{y}=1)&= \frac{p^{\text{ref}}(\mathbf{x}_T)p(\mathbf{y}=1 \vert \mathbf{x}_T)}{\sum_{\mathbf{x}_T} p^{\text{ref}}(\mathbf{x}_T)p(\mathbf{y}=1 \vert \mathbf{x}_T)} \\ &= \frac{p^{\text{ref}}(\mathbf{x}_T)\frac{1}{M}\frac{\tilde{\pi}_T(\mathbf{x}_T)}{p^{\text{ref}}(\mathbf{x}_T)}}{\sum_{\mathbf{x}_T} p^{\text{ref}}(\mathbf{x}_T)\frac{1}{M}\frac{\tilde{\pi}_T(\mathbf{x}_T)}{p^{\text{ref}}(\mathbf{x}_T)} } \\ &= \frac{\tilde{\pi}_T(\mathbf{x}_T)}{\sum_{\mathbf{x}_T}\tilde{\pi}_T(\mathbf{x}_T) } \\ &= \pi_T(\mathbf{x}_T). \end{align*} $$ ).

Again, we emphasize that this construction is hypothetical and does not affect algorithm design. Nevertheless, it is useful to add detail to presentation in the influential 2018 tutorial by Sergey Levine and facilitate our unified viewpoint in terms of posterior inference.

Initial Sampling

An immediate question arises as to how to initialize sampling in \eqref{eq:backward}, since \(p^*(\mathbf{x}_{0} \vert \mathbf{y})\) is already likely to be intractable in general.

In language modeling settings, we are often given access to prompts $\mathbf{x}_{0}$ via data or user interaction, so it is natural to focus on the posterior over responses to particular prompts,

\[\begin{align} p^*(\mathbf{x}_{1:T} \vert \mathbf{x}_{0}, \mathbf{y}) &= \frac{1}{\mathcal{Z}^{\mathbf{y}}_0(\mathbf{x}_{0})} p^{\text{ref}}(\mathbf{x}_{1:T}|\mathbf{x}_{0}) p(\mathbf{y} \vert \mathbf{x}_T) \label{eq:tgt2} \\ \mathcal{Z}^{\mathbf{y}}_{0}(\mathbf{x}_{0}) &=\int p^{\text{ref}}(\mathbf{x}_{1:T}|\mathbf{x}_{0})p(\mathbf{y} \vert \mathbf{x}_T) d\mathbf{x}_{1:T} \nonumber \end{align}\]

However, in diffusion models, we remain interested in \(p^*(\mathbf{x}_{0:T} \vert \mathbf{y})\), and risk introducing bias if our initial sampling distribution differs from $p^*(\mathbf{x}_{0} \vert \mathbf{y})$. It may be possible to sample from \(p^*(\mathbf{x}_{0} \vert \mathbf{y}) \approx p^{\text{ref}}(\mathbf{x}_{0})\) in cases when the noising dynamics converge quickly to a stationary distribution, such as a standard Normal, regardless of the initial distribution . Similarly, finetuning could be performed using a `memoryless’ noise schedule which renders \(p^{\text{ref}}(\mathbf{x}_T|\mathbf{x}_{0}) = p^{\text{ref}}(\mathbf{x}_T)\) and thus \(p^*(\mathbf{x}_{0} \vert \mathbf{y})= p^{\text{ref}}(\mathbf{x}_{0})\) . We proceed to assume \(\mathbf{x}_{0} \sim p^*(\mathbf{x}_{0} \vert \mathbf{y})\) in the diffusion setting, and focus on subsequent sampling steps for \(p^*(\mathbf{x}_{1:T} \vert \mathbf{x}_{0}, \mathbf{y})\) to encompass both language and diffusion settings.

Soft Value Function

We begin by characterizing the target posterior \(p^*(\mathbf{x}_{1:T} \vert \mathbf{x}_{0}, \mathbf{y})\) via the solution to a variational optimization, which we will refer to as an Evidence Lower Bound (ELBO),

\(\begin{align} V^{\mathbf{y}}_{0}(\mathbf{x}_{0}) &= \max \limits_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} ~ \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})}\big[ \log p(\mathbf{y}\vert \mathbf{x}_{T}) \big] - D_{KL}\big[q(\mathbf{x}_{1:T}|\mathbf{x}_{0}): p^{\text{ref}}(\mathbf{x}_{1:T}|\mathbf{x}_{0})\big] \label{eq:elbo} \\ &= \log \mathcal{Z}^{\mathbf{y}}_{0}(\mathbf{x}_{0}) \nonumber \end{align}\) The posterior \(q(\mathbf{x}_{1:T}|\mathbf{x}_{0})= p^*(\mathbf{x}_{1:T} | \mathbf{x}_{0}, \mathbf{y}) = \frac{1}{\mathcal{Z}^{\mathbf{y}}_{0}(\mathbf{x}_{0})} p^{\text{ref}}(\mathbf{x}_{1:T}|\mathbf{x}_{0}) p(\mathbf{y}|\mathbf{x}_T)\) achieves the maximum. This can seen by solving for the the optimal $q$, subject to a normalization constraint. Taking the variation with respect to $q$, $$\begin{align*} \frac{\delta}{\delta q}[\cdot] = \log p(\mathbf{y}\vert \mathbf{x}_{T}) - \log q(\mathbf{x}_{1:T}|\mathbf{x}_{0}) + \log p^{\text{ref}}(\mathbf{x}_{1:T}|\mathbf{x}_{0}) - 1 - \lambda(\mathbf{x}_0) = 0 \\ \implies q^*(\mathbf{x}_{1:T} | \mathbf{x}_{0}) = \frac{1}{\mathcal{Z}^{\mathbf{y}}_{0}(\mathbf{x}_{0})}p^{\text{ref}}(\mathbf{x}_{1:T}|\mathbf{x}_{0}) p(\mathbf{y}\vert \mathbf{x}_{T}) \end{align*}$$ Plugging back into \eqref{eq:elbo} and cancelling terms, we see that the soft value function corresponds to the log normalization constant \(V^{\mathbf{y}}_{0}(\mathbf{x}_{0}) = \log \mathcal{Z}^{\mathbf{y}}_{0}(\mathbf{x}_{0})\).

The optimal soft value function can be understood as translating terminal target information to intermediate steps, which facilitates sampling the exact posterior marginals along the entire trajectory. In particular, consider the optimization \eqref{eq:elbo} starting from a given partial sequence or intermediate state \(\mathbf{x}_t\),

\[\begin{align} \hspace{-.25cm} V^{\mathbf{y}}_{t}(\mathbf{x}_t) &= \max \limits_{q(\mathbf{x}_{t+1:T}\vert \mathbf{x}_{t})} ~ \mathbb{E}_{q(\mathbf{x}_{t+1:T}\vert \mathbf{x}_{t})}\big[ \log p(\mathbf{y}\vert \mathbf{x}_{T}) \big] - D_{KL}\big[q(\mathbf{x}_{t+1:T}\vert \mathbf{x}_{t}): p^{\text{ref}}(\mathbf{x}_{t+1:T} \vert \mathbf{x}_{t})\big] \label{eq:elbot} \\ &=\log \int p^{\text{ref}}(\mathbf{x}_{t+1:T}\vert \mathbf{x}_{t}) p(\mathbf{y}\vert \mathbf{x}_{T}) d\mathbf{x}_{t+1:T} \label{eq:int_value} \\ &= \log p^*(\mathbf{y} \vert \mathbf{x}_t) \label{eq:cond_lkd} \end{align}\]

The soft value function measures the expected target likelihood under rollouts from the reference policy, which may involve generating tokens \(x_{t+1:T}\) or running diffusion sampling until time \(T\). In our setting with no intermediate reward or target information, we can recognize the expression for $V_{\mathbf{y}}^*(\mathbf{x}_t)$ in \eqref{eq:int_value} as a conditional likelihood in \eqref{eq:cond_lkd} We will find rich applications in our the setting of no intermediate reward or targets, but refer the interested reader to , , for discussion of this case in various settings.

One-Step Optimal Policy

Similarly, we can write the one-step-ahead posterior transitions using soft values,

\[\begin{align} p^*(\mathbf{x}_{t} \vert \mathbf{x}_{t-1}, \mathbf{y}) &= p^{\text{ref}}(\mathbf{x}_{t}|\mathbf{x}_{t-1}) \frac{p^*(\mathbf{y} \vert \mathbf{x}_t)}{p^*(\mathbf{y} \vert \mathbf{x}_{t-1})} \nonumber \\ &= p^{\text{ref}}(\mathbf{x}_{t}|\mathbf{x}_{t-1}) \exp\{ V^{\mathbf{y}}_{t}(\mathbf{x}_{t}) - V^{\mathbf{y}}_{t-1}(\mathbf{x}_{t-1}) \} \label{eq:next_token} \end{align}\]

where \(V^{\mathbf{y}}_{t-1}(\mathbf{x}_{t-1}) = \log \mathcal{Z}^{\mathbf{y}}_{t-1} (\mathbf{x}_{t-1})\) again is the log normalization constant.

Intermediate Marginal Distributions

Finally, composing the optimal one-step policies above, we can consider how the target marginal distribution of \(\mathbf{x}_t\) evolves over time. In terms of the soft value function, we have

\(\begin{align} p^*_{t}(\mathbf{x}_{t}\vert \mathbf{x}_{0}, \mathbf{y}) = \frac{1}{\mathcal{Z}^{\mathbf{y}}_{0}(\mathbf{x}_{0})} p^{\text{ref}}(\mathbf{x}_{t}|\mathbf{x}_{0}) \exp\{ V_\mathbf{y}^*(\mathbf{x}_{t}) \} \label{eq:marginal} \end{align}\)

where \(\mathbf{x}_0\) conditioning only affects the \(p^{\text{ref}}\) term. We can equivalently express \eqref{eq:marginal} using likelihood ratios or logits, \(\begin{align} \log \frac{p^*(\mathbf{x}_{t} \vert \mathbf{x}_{0}, \mathbf{y})}{p^{\text{ref}}(\mathbf{x}_{t} | \mathbf{x}_{0})} = V^{\mathbf{y}}_{t}(\mathbf{x}_{t}) - V^{\mathbf{y}}_{0}(\mathbf{x}_{0}) = \log p^*(\mathbf{y} \vert \mathbf{x}_t) - \log \mathcal{Z}^{\mathbf{y}}_{0}(\mathbf{x}_{0}) \label{eq:logits} \end{align}\)

The central message is that the optimal soft value function provides a “backward message” summarizing future conditioning information relevant to sampling at time $t$.

Stochastic Optimal Control

Remarkably, the gradient of the soft value function can also be shown to provide the optimal drift for a controlled diffusion process guiding samples to the endpoint target distribution.
To build up to this connection, we note that in the continuous-time limit, the KL divergence in \eqref{eq:elbo} is finite only for path measures or SDEs of the form

\[\begin{align} Q^{u}: \quad d\mathbf{x}_t = \left( b_t^{\text{ref}}(\mathbf{x}_t ) + u_t(\mathbf{x}_t ) \right) dt + \sigma_t dW_t, \label{eq:csde} \end{align}\]

where $u_t$ satisfies mild regularity condtiions. In this case, the KL divergence can be written as the time-integral of the norm of \(u_t\) using the Girsanov theorem, and we can recognize the negative of the ELBO in \eqref{eq:elbo} as a stochastic optimal control problem

\[\begin{align} - V^\mathbf{y}_{0}(\mathbf{x}_{0}) = \min \limits_{Q^u(\mathbf{x}_{(0,T]}|\mathbf{x}_{0})} ~ \mathbb{E}_{Q^u(\mathbf{x}_{0:T})}\Big[ - \log p(\mathbf{y}\vert \mathbf{x}_{T}) + \int_{0}^T \frac{1}{2\sigma_t^2}\|u_t(\mathbf{x}_t)\|^2 dt \Big] \label{eq:soc} \end{align}\]

subject to \(Q^u\) having the form of \eqref{eq:csde}. Using variational calculus, See Sec. 2 and Appendix for accessible derivations. one can show that the solution takes the form

\(\begin{align} u_t(\mathbf{x}_t) = \sigma_t^2 \nabla_{\mathbf{x}_t} V^{\mathbf{y}}_t(\mathbf{x}_t) = \sigma_t^2 \nabla_{\mathbf{x}_t} \log p^*(\mathbf{y}|\mathbf{x}_t) \label{eq:soft_value_drift} \end{align}\)

Using the probabilistic view of the value functions in \eqref{eq:int_value}-\eqref{eq:cond_lkd}, observe that the exponentiated value functions are related via expectations under the reference process

\[\begin{align} \exp\{ V^{\mathbf{y}}_t(\mathbf{x}_t) \} = \mathbb{E}_{p^{\text{ref}}(\mathbf{x}_{t+s} \vert\mathbf{x}_{t})}\left[ \exp\{ V^{\mathbf{y}}_{t+s}(\mathbf{x}_{t+s}) \} \right] \label{eq:value_martingale} \end{align}\]

This is known as a martingale condition in the stochastic process literature, where \(h_t^{\mathbf{y}} = \exp\{ V_t^{\mathbf{y}} \}\) is often known as Doob’s $h$-function. The martingale condition ensures that conditional and marginals constructed from \eqref{eq:next_token}-\eqref{eq:marginal} are consistent with respect to marginalization, and results in the following remarkable theorem .

Theorem 1 For any function satisfying \eqref{eq:value_martingale}, the stochastic process

\[\begin{align} d\mathbf{x}_t = \left( b_t^{\text{ref}}(\mathbf{x}_t ) + \sigma^2 \nabla V_t(\mathbf{x}_t ) \right) dt + \sigma_t dW_t \end{align}\]

realizes the transition dynamics

\[\begin{align} p^V(\mathbf{x}_{t+s} | \mathbf{x}_t) = \frac{\exp\{ V_{t+s}(\mathbf{x}_{t+s})\} }{\exp\{ V_t(\mathbf{x}_t)\}} p^{\text{ref}}(\mathbf{x}_{t+s} | \mathbf{x}_t) \end{align}\]

This theorem is true for any function satisfying the martingale condition, including the optimal value function corresponding to a particular target $p^*$, and demonstrates the link between value functions, guidance drifts for controlled diffusion processes, and posterior or conditioned transition probabilities.

Twisted Sequential Monte Carlo Sampling

In both the language and diffusion cases, we can leverage Sequential Monte Carlo to resample a set of $K$ partial sequences or intermediate states based on the (optimal) soft values, which has the effect of prioritizing sequences or states which we expect to achieve high likelihood under the final-step target distribution.

To introduce this importance sampling technique, we consider the unnormalized \(\tilde{p}^{*}(\mathbf{x}_{1:T} \vert \mathbf{x}_0, \mathbf{y}) = p^{\text{ref}}(\mathbf{x}_{1:T} \vert \mathbf{x}_{0}) p(\mathbf{y} \vert \mathbf{x}_T)\) (see \eqref{eq:tgt2}), which omits the intractable normalization constant \(\mathcal{Z}^\mathbf{y}_0(\mathbf{x}_0)\) and thus is easy to evaluate. For a given proposal or approximate posterior \(q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)\) (which may be learned as in Objectives below, or simply set to \(p^{\text{ref}}\) ), consider the importance weights in the extended space,

\[\begin{align} w_{1:T}(\mathbf{x}_{1:T}) = \frac{\tilde{p}^*(\mathbf{x}_{1:T}|\mathbf{x}_0,\mathbf{y})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}, \qquad \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}\left[ w_{1:T}(\mathbf{x}_{1:T}) \right] = \mathcal{Z}^\mathbf{y}_0(\mathbf{x}_0) \label{eq:unbiased} \end{align}\]

The latter equality suggests that the weights are an unbiased estimator of the intractable normalization constant \(\mathcal{Z}^\mathbf{y}_0\), assuming \(w_{1:T} < \infty\) for all \(\mathbf{x}_{1:T}\).

We would like to transform these weights into step-by-step incremental weights which will allow us to perform importance-weighting of intermediate states according to the optimal target posterior. While a naive forward factorization \(w_{1:T}(\mathbf{x}_{1:T}) = p(\mathbf{y} \vert \mathbf{x}_T) \prod_{t=1}^T \frac{ p^{\text{ref}}(\mathbf{x}_{t} \vert \mathbf{x}_{t-1})}{q(\mathbf{x}_{t} \vert \mathbf{x}_{t-1})}\) would only include target information at the final step, we should instead consider the posterior transitions in \eqref{eq:backward}. Rewriting \(p^{*}(\mathbf{x}_{t} \vert \mathbf{x}_{t-1}, \mathbf{y}) = \frac{p^*(\mathbf{y} \vert \mathbf{x}_t)}{p^*(\mathbf{y} \vert \mathbf{x}_{t-1})} p^{\text{ref}}(\mathbf{x}_{t} \vert \mathbf{x}_{t-1})\) using \eqref{eq:next_token}, we have

\[\begin{align} w_{1:T}(\mathbf{x}_{1:T}) &= \prod_{t=1}^T \frac{p^*(\mathbf{x}_{t} \vert \mathbf{x}_{t-1}, \mathbf{y})}{q(\mathbf{x}_{t} \vert \mathbf{x}_{t-1})} \nonumber \\ &= \prod_{t=1}^T \frac{p^*(\mathbf{y} \vert \mathbf{x}_t)}{p^*(\mathbf{y} \vert \mathbf{x}_{t-1})} \frac{p^{\text{ref}}(\mathbf{x}_{t} \vert \mathbf{x}_{t-1})}{q(\mathbf{x}_{t} \vert \mathbf{x}_{t-1})} = \prod_{t=1}^T \frac{\exp\{ V^{\mathbf{y}}_{t}(\mathbf{x}_{t}) \}}{\exp\{ V^{\mathbf{y}}_{t-1}(\mathbf{x}_{t-1}) \}} \frac{p^{\text{ref}}(\mathbf{x}_{t} \vert \mathbf{x}_{t-1})}{q(\mathbf{x}_{t} \vert \mathbf{x}_{t-1})} \label{eq:weights} \end{align}\]

Note,the numerator at the final step includes the given target conditional \(p(\mathbf{y} \vert \mathbf{x}_T)\).

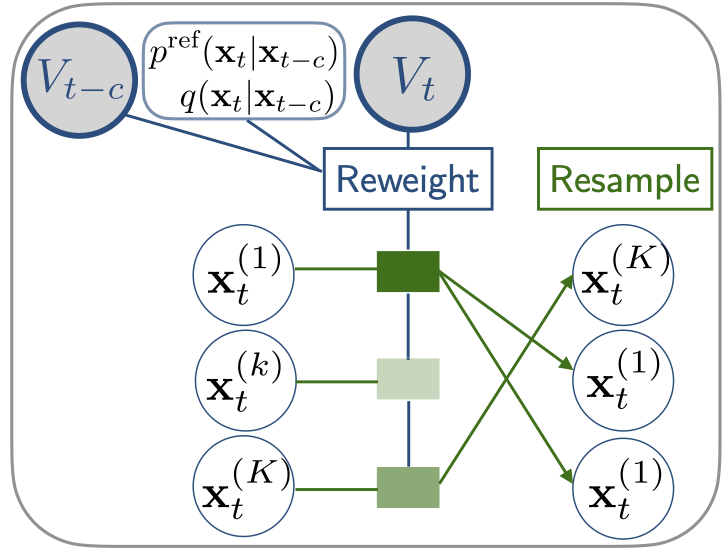
The weights in \eqref{eq:weights} suggest a sequential resampling scheme at intermediate steps. For a budget of \(K\) samples and looping over timesteps \(1 \leq t \leq T\), we can proceed with the following steps:

• for \(t \in [1, T]\):
  • for \(k \in [1, K]\):
    • Sample \(\mathbf{x}_t^{(k)} \sim q(\mathbf{x}_t \vert \mathbf{x}_{t-1}^{(k)})\)
    • Update weights \(w_{1:t}^{(k)} = w_{1:t-1}^{(k)} \frac{p^*(\mathbf{y} \vert \mathbf{x}_t^{(k)})}{p^*(\mathbf{y} \vert \mathbf{x}_{t-1}^{(k)})} \frac{p^{\text{ref}}(\mathbf{x}_{t}^{(k)} \vert \mathbf{x}_{t-1}^{(k)})}{q(\mathbf{x}_{t}^{(k)} \vert \mathbf{x}_{t-1}^{(k)})}\)
  • (if resampling condition met, perform multinomial resampling):
    • Sample \(i_k \sim \text{categorical}\left( \Big\{ \frac{w_{1:t}^{(j)}}{\sum_{j=1}^K w_{1:t}^{(\ell)}} \Big\}_{j=1}^K \right)\) for \(k \in [1,K]\)
    • Copy or Reassign Samples: \(\mathbf{x}_t^{(k)} \gets \mathbf{x}_t^{(i_k)}\) ( for all \(k \in [1,K]\) in parallel)
    • Reset weights: \(w_{1:t}^{(k)} \gets \frac{1}{K} \sum_{j=1}^K w_{1:t}^{(j)}\)

Note that resetting the weights means that only subsequent weights are used for resampling at future timesteps, which preserves the unbiasedness of the eventual weights in \eqref{eq:unbiased}. See the blog post by Tuan Anh Le for an elegant proof . More advanced resampling techniques such as systematic resampling might also be used.

Finally, we can use this resampling scheme even for approximate \(V^{\theta}_{t}(\mathbf{x}_{t})\) or \(p^\theta(\mathbf{y} \vert \mathbf{x}_{t})\) for \(t < T\), although it is clear that the efficacy of this scheme will depend on the quality of these intermediate value functions or likelihoods.

Language

For the language modeling setting, recall that we absorbed the autoregressive model into Markov transitions \(p^{\text{ref}}(\mathbf{x}_{t} \vert \mathbf{x}_{t-1})=p^{\text{ref}}_{\text{LM}}(x_{t} \vert \mathbf{x}_{t-1}) \mathbb{I}[\mathbf{x}_{t} =\text{concat}(\mathbf{x}_{t-1}, x_{t})]\) where the states expand with concatenation of next tokens. Rewriting the proposal in similar terms, we can think of the weights as evolving according to

\[\begin{align} w_{1:T}(\mathbf{x}_{1:T}) &= \prod_{t=1}^T \frac{p(\mathbf{y} \vert \mathbf{x}_t)}{p(\mathbf{y} \vert \mathbf{x}_{t-1})} \frac{p^{\text{ref}}_{\text{LM}}(x_t \vert \mathbf{x}_{t-1})}{q_{\text{LM}}(x_t \vert \mathbf{x}_{t-1})} = \prod_{t=1}^T \frac{\exp\{ V^{\mathbf{y}}_{t}(\mathbf{x}_{t}) \}}{\exp\{ V^{\mathbf{y}}_{t-1}(\mathbf{x}_{t-1}) \}} \frac{p^{\text{ref}}_{\text{LM}}(x_t \vert \mathbf{x}_{t-1})}{q_{\text{LM}}(x_t \vert \mathbf{x}_{t-1})} \nonumber \end{align}\]

where the likelihood or values are evaluated on the partial sequences \(\mathbf{x}_t\) and \(\mathbf{x}_{t-1}\). See or for additional discussion.

Diffusion

Since diffusion process operate on states \(\mathbf{x}_{t} \in \mathbb{R}^d\) in Markovian fashion, the weights in \eqref{eq:weights} can be used as is, where \(q(\mathbf{x}_{t} \vert \mathbf{x}_{t-1})\) corresponds to the discretization of a stochastic process as in \eqref{eq:csde}.

Objective Functions

We finally discuss several classes of objective functions for learning value functions and/or approximate posterior policies. We only attempt to give a high-level landscape of various methods, mostly in discrete time, and defer to references for algorithmic and technical details.

Evidence Lower Bound (Mode-Seeking KL)

Similarly to derivations in the case of standard variational inference, one can show that, for a given \(q\), the gap in the ELBO in \eqref{eq:elbo} is the mode-seeking KL divergence \(D_{KL}\big[ q(\mathbf{x}_{1:T} | \mathbf{x}_{0}) : p^*(\mathbf{x}_{1:T} | \mathbf{x}_{0}, \mathbf{y})\big]\). Thus, minimizing this KL divergence corresponds to maximizing \eqref{eq:elbo}. Notably, since \(q(\mathbf{x}_{1:T} | \mathbf{x}_{0})\) appears in the first argument, optimizing this objective requires taking gradients through the sampling procedure.

Language

When \(\log p(\mathbf{y}\vert \mathbf{x}_{T}) = \beta ~ r(\mathbf{x}_{T}) - \log M\) , we recognize \eqref{eq:elbo} as a common objective for reinforcement learning from human feedback in language models, where \(q(\mathbf{x}_{1:T}|\mathbf{x}_0)\) is optimized using policy gradient methods such as PPO or REINFORCE . While PPO maintains a value network to reweight policy gradients, the focus is on finetuning a policy \(q^{\phi}(\mathbf{x}_{1:T}|\mathbf{x}_0)\), and an optimal policy \(q = p^*\) will implicitly capture the value functions through the next-token logits in \eqref{eq:next_token}. A similar observation underlies token-wise interpretations of direct preference optimization parameterizations . Nevertheless, learned value functions may also be used to guide generative sampling, either through Monte Carlo Tree Search or Sequential Monte Carlo (as above).

Diffusion

Methods for solving stochastic control problems have an extensive history dating back to . Directly solving \eqref{eq:soc} using backpropagation through trajectories is known as the adjoint method , for which improved gradient estimators have been recently proposed in . The adjoint method was used for sampling from general unnormalized target densities in .

Cross Entropy (Mass-Covering KL)

While the ELBO and mode-seeking KL divergence was used to introduce the target distribution as the solution of a variational optimization in \eqref{eq:elbo}, we can perform optimization using any divergence minimization technique with the desired optimum. One example is to optimize the mass-covering KL divergence as in maximum likelihood training of energy-based models, where recognizing the form of the optimal target marginals in \eqref{eq:marginal}, we optimize

\[\begin{align} \min \limits_{\theta} \sum_{t=1}^T D_{KL}\big[ p^*(\mathbf{x}_{1:t} \vert \mathbf{x}_{0}, \mathbf{y}) : p^{\text{ref}}(\mathbf{x}_{1:t} \vert \mathbf{x}_{0}) \exp\{V^\theta_t(\mathbf{x}_t) \}/\mathcal{Z}_{V^\theta}(\mathbf{x}_0) \big] \end{align}\]

Although exact samples from \(p^*(\mathbf{x}_{1:t} \vert \mathbf{x}_{0}, \mathbf{y})\) are usually not available, one may use importance sampling approximations to reweight samples according to the endpoint target information \(p(\mathbf{y} \vert \mathbf{x}_T )\), and reuse these weights for approximate sampling at intermediate \(t\).

Language

For full-sequence policy optimization with the only loss at the final-step \(T\), the distributional policy gradient algorithm amounts to optimizing the mass-covering KL, where the energy is parameterized directly via a normalized policy \(q^{\phi}(\mathbf{x}_{1:T} \vert \mathbf{x}_0)\). For learning intermediate value functions, contrastive twist learning optimizes a marginal KL divergence at each step, learning the value functions \(V^{\mathbf{y}}_{t}\) as energies.

Diffusion

The contrastive energy prediction objective in amounts to approximate energy-based training of the value functions \(V^{\mathbf{y}}_{t}\) at each step, which can then be used to guide sampling using \(\nabla V^{\mathbf{y}}_{t}\) as a guidance or control drift in \eqref{eq:csde}.

For sampling from a general target density, learn intermediate value functions for guidance and SMC resampling using a `target score matching’ loss . This loss requires importance sampling corrections to draw approximate samples from the endpoint target distribution \(p^{*}(\mathbf{x}_T \vert \mathbf{y})\) (as in the mass-covering KL), but the loss directly regresses against the gradient of the target energy or log unnormalized density.

Path Consistency

Path Consistency objectives consider enforcing the first-order optimality conditions associated with the optimization in \eqref{eq:elbo}-\eqref{eq:elbot} using a squared error loss. Since this is a functional equality which should hold everywhere, we can optimize the loss over some off-policy sampling distribution \(\pi_s(\mathbf{x}_{1:T}\vert\mathbf{x}_0)\). Taking the variation of \eqref{eq:elbo}-\eqref{eq:elbot} with respect to \(q\) yields a KKT condition, which we can enforce using

\[\begin{align} \min \limits_{\theta,\phi} \mathbb{E}_{\pi_s(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}\left[\left( \log p(\mathbf{y}\vert \mathbf{x}_{T}) - V^{\theta}_{0}(\mathbf{x}_0) - \log \frac{q^\phi(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})}{p^{\text{ref}}(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} \right)^2 \right] \end{align}\]

This may also be viewed as minimizing the square of the log importance weights between full-sequence forward and reverse processes in \eqref{eq:unbiased}-\eqref{eq:weights}. Note that we may also construct one- or $c$-step consistency losses for any \(1 \leq t \leq t + c \leq T\) using the compositional structure of the optimal values in \eqref{eq:elbot}-\eqref{eq:marginal} or decomposition of weights in \eqref{eq:weights},

\[\begin{align} \min \limits_{\theta,\phi} \mathbb{E}_{\pi_s(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}\left[\left( V^{\theta}_{t+c}(\mathbf{x}_{t+c}) - V^{\theta}_{t}(\mathbf{x}_t) - \sum_{\tau=t+1}^{t+c} \log \frac{q^\phi(\mathbf{x}_{\tau} \vert \mathbf{x}_{\tau-1})}{p^{\text{ref}}(\mathbf{x}_{\tau} \vert \mathbf{x}_{\tau-1})} \right)^2 \right] \end{align}\]

Non-zero intermediate rewards would also appear in the loss.

Language

Path consistency losses correspond to (partial) `trajectory balance’ losses in the literature on Generative Flow networks (GFlowNets), and have been applied for inference and finetuning in autoregressive language models.

Diffusion

Trajectory balance or path consistency losses can also be applied for inference in diffusions models , see also . In the sampling literature, a similar principle underlies the log-variance divergences studied in , in which we enforce that the log likelihood ratio of path-measures or stochastic processes be constant or equal to zero. Recent work has also married these losses with intermediate SMC resampling.

Denoising Mean Approximation for Diffusion Settings

Diffusion models parameterized via denoising mean prediction \(\hat{\mathbf{x}}_T = D_\theta(t,\mathbf{x}_t)\) provide a particularly convenient, training-free estimator of intermediate value functions. Instead of fully estimating the expectation in \eqref{eq:int_value} or \eqref{eq:value_martingale}, one can make a single-sample approximation by evaluating \(p(\mathbf{y}\vert \hat{\mathbf{x}}_T)\) at the denoising mean prediction,

\[\begin{align} V^{\mathbf{y}}_t(\mathbf{x}_t) = \log \mathbb{E}_{p^{\text{ref}}(\mathbf{x}_{T} \vert\mathbf{x}_{t})}\left[ p(\mathbf{y}\vert\mathbf{x}_T) \right] \approx \log p(\mathbf{y}\vert\hat{\mathbf{x}}_T) \end{align}\]

From this approximation, we can construct an approximate guidance drift \(\nabla \hat{V}^{\mathbf{y}}_t(\mathbf{x}_t) \approx \nabla \log p(\mathbf{y}\vert\hat{\mathbf{x}}_T)\) (for differentiable likelihoods) along with targets \(\hat{V}^{\mathbf{y}}_t(\mathbf{x}_t)\) for intermediate SMC resampling in \eqref{eq:weights} . This approximation has found wide applicability for inverse problems , protein generation , and images for continuous diffusion models, along with recent applications for discrete diffusion models . However, given that this estimator can be crude even in simple cases , recent work finds benefits to annealing the contribution of these terms for both guidance and SMC.

Conclusion

In this blog post, we have proposed to understand controlled generation, sampling, and guidance in both language and diffusion models through the lens of probabilistic inference. Through connections with soft reinforcement learning and stochastic optimal control, we obtain a rich design space of objective functions for learning both approximate posterior distributions and value functions, which can also be used within sequential importance sampling techniques to improve generation and estimation. We hope that this overview provides useful conceptual tools for newcomers to these rapidly-evolving areas, while also contributing to the continued cross-pollination of ideas (i) between language and diffusion model literatures, (ii) between particular problem settings within the diffusion literature, or (iii) between sampling, RL, and finetuning literatures.Thanks to Yuanqi Du for feedback on a draft of this post.